Una de las mejores formas de utilizar R es para análisis estadísticos de todo tipo. Una de las operaciones estadísticas más frecuentes que nos puede interesar y que en R son triviales es la regresión lineal.
Este pequeño script nos permite importar datos extraídos de un CSV (aunque podríamos extraerlo de un .TXT o cualquier otro formato), que antes hemos exportado desde cualquier web de datos (el INE, OCDE o Eurostat permite descargar los datos directamente en CSV) o que hemos exportado desde cualquier programa como Excel o Open Office o Google Drive. Después de importarlo este script generará un “plot” o gráfica con los datos que hemos aportado, incluyendo una línea de regresión y un resumen estadístico que podremos incluir bajo la gráfica allí donde vayamos a publicarla o incluso incluir algunos pequeños datos descriptivos adicionales (ver notas al final del programa).
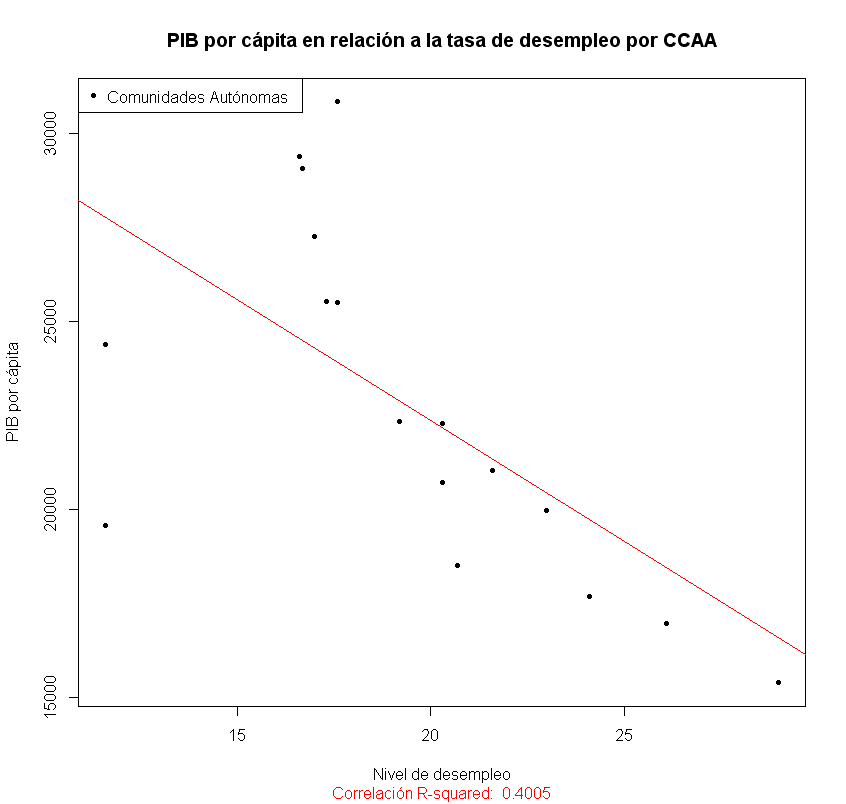
El resultado es conseguir gráficas de este tipo:
Y datos estadísticos completos de una correlación como estos:
[1] “Ecuación de regresión”
lm(formula = datos[, 2] ~ datos[, 1])
Residuals:
Min 1Q Median 3Q Max
-8195.3 -1487.8 -475.4 1599.4 6920.4Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 35215.6 4044.4 8.707 2.99e-07 ***
datos[, 1] -642.4 202.9 -3.166 0.0064 **
—
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1Residual standard error: 3708 on 15 degrees of freedom
Multiple R-squared: 0.4005, Adjusted R-squared: 0.3605
F-statistic: 10.02 on 1 and 15 DF, p-value: 0.006399[1] “Correlación entre variables”
Nivel.de.desempleo PIB.por.cÃ.pita
Nivel.de.desempleo 1.0000000 -0.6328501
PIB.por.cÃ.pita -0.6328501 1.0000000
Script regresion-plot.R
############# Objetivo del programa ###############################
## Nombre: Construcción de una gráfica de dispersión con línea de regresión
##
## Objetivo: Función que utiliza un fichero de exportación .csv
##para construir una gráfica de dispersión
## y dibuja la línea de regresión, incluyendo el valor de R
##
## Descripción: Exporto los contenidos de una tabla Excel o
## cualquier otra fuente y lo exporto en formato CSV,
## separado con ",". Este input lo importo y hago un análisis
## de regresión lineal y lo plasmo en una gráfica.
##
## Preparación del CSV: Este ha de incluir en la primera columna
## con datos la variable que quiero que esté en la X y en la
## segunda columna la variable que quiero que esté en la Y
##
## De cara a la regresión consideraré la y dependiente de x
## Es decir y = f(x), en este caso linear y ~ x
##
## Output: Una imagen con la gráfica y un resumen de la
## signficación estadísticade la regresión
##
## Sistema en el que está testeado:
## R-Studio confuncionando bajo Windows-XP SP3
###################################################################
###############################################
## Variables
############################################
nombrearchivo = "paro-pib.csv" ## el nombre del archivo CSV que extraigo
descripcion1 = "Nivel de desempleo" ## Descripción de la variable 1 que pondré en el eje X
descripcion2 = "PIB por cápita" ## Descripción de la variable 2 que pondré en el eje y
titulo = "PIB por cápita en relación a la tasa de desempleo por CCAA" ## Título de la gráfica
################### Inicio del programa #####################
## header= TRUE si el CSV exporta los header, sino eliminarlo
## rownames= 1 si el CSV incluye descriptores en cada línea en la primera columna, sino eliminarlo.
datos = read.table(nombrearchivo, sep=",", header=TRUE, row.names=1) ##(,)
print ("Resumen de la tabla")
print (head(datos)) ### Asi logro imprimir una versión resumida de los datos en la consola
regresion = lm(datos[,2] ~ datos[,1]) ## Construyo una ecuación de regresión lineal
## existe una opción más general para modelos lineales generales.
## Podemos sustituir la línea anterior por esta
# regresion = glm(datos[,2] ~ datos[,1])
##
############################################
##### Hago el plot, o sea, la gráfica ######
############################################
pairs(datos) ### esto crea un plot previo que permite ver la correlación de forma visible de las variables
plot(datos[,1], datos[,2], xlab = descripcion1, ylab = descripcion2, pch=20) ## plot principal de dispersión
abline (regresion, lwd=1, col ="red" ) ### Dibujo la línea de regresión
title (titulo) ## Añado un título al gráfico
########################################
## Imprimo en la consola algunos datos que nos pueden ser útiles
##############
print ("Ecuación de regresión")
print(summary(regresion)) ## Me extrae un resumen estadístico del valor de regresión
print ("Correlación entre variables")
print(cor (datos)) ### Nos dara un índice de correlación entre las diversas variables
##################################################################
################## Cosas que puedo añadir al gráfico #############
## Si quiero incluir los datos estadísticos en la parte inferior
## puedo incluir esta línea en la consola:
# title (sub="Multiple R-squared: 0.4005", col.sub="red")
##
##
## Le puedo añadir una leyenda
# legend("topleft", legend="Comunidades autónomas", pch=20)
##
###################################
## Luego puedo exportar el archivo a PNG con la propia herramienta ## de R.
Si después quiero comprobar la robustez de la regresión puedo añadir unos cuantos pasos desde la consola para analizar el residuo de la regresión.
anova(regresion) ## tendré un análisis de varianza residuos = rstandard(regresion) valores.ajustados = fitted(regresion) plot(valores.ajustados, residuos) qqnorm(residuos) qqline(residuos)
Con esto conseguiré un análisis de varianza y una forma gráfica de visualizar el residuo de la regresión versus la proyección teórica de esta.
Otras regresiones
Para conseguir regresiones no lineales, tenemos que hacer las siguientes modificaciones:
Regresión logarítmica
Modifico la definición de la función regresion. Y en la operación de “plot”.
### Modificaré la regresion por esta nueva definición regresion = lm(log(datos[,2]) ~ datos[,1]) ## La regresión la haremos sobre el logaritmo de la segunda columna## , la dependiente. ### Cuando haga el plot, he de recordar hacerlo sobre el logaritmo ## de la segunda columna plot(log(datos[, 2]) ~ datos[, 1], xlab = descripcion1, ylab = descripcion2, pch=20) ## plot principal de dispersión ## He de poner algo en el título que me indique que es una ## regresion linear titulo = "Regresión logarítmica de PIB vs. paro" ## O bien ponerlo en el descriptor 2 descripcion2 = "Log(PIB por cápita)"
Regresiones lineales multivariables
Imaginemos que tenemos un CSV con varias columnas con datos, la 1, la 2, la 3 y la 4 que es nuestra variable dependiente
#### La importación, etc... sigue siendo igual, ### Tendremos que ampliar variables al inicio del programa descripcion3 = "Segunda variable independiente" descripcion4 = "Tercera variable independiente" ### Nuestra regresión adquirirá esta forma regresion = lm(datos[,4] ~ datos[,1] + datos[,2] + datos[,3]) ############ Construir el plot se vuelve algo más complejo ## Puedo optar por poner un solo plot con tres gráficos ## ## esto se hace definiendo el número de plots en 3 filas por una ## columna par(mfrow=c(3,1)) ## Haremos que el #### Dibujo los 3 plots ##### plot(datos[,1], datos[,2], xlab = descripcion1, ylab = descripcion2, pch=20) ## plot1 principal de dispersión abline (regresion) plot(datos[,3], datos[,2], xlab = descripcion3, ylab = descripcion2, pch=20) ## plot2 principal de dispersión abline (regresion) plot(datos[,4], datos[,2], xlab = descripcion4, ylab = descripcion2, pch=20) ## plot3 principal de dispersión abline (regresion, color="red")
¿Qué aporta este tutorial?
Siendo uno de los scripts más sencillos que se pueden hacer en R, y existiendo tutoriales tan excelentes como este (del cuál hay elementos que he utilizado en mi tutorial), he querido prepararlo en forma de plantilla reutilizable ya que así facilito el trabajo para encontrar correlaciones de forma rápida sin tener que preocuparme de tener que modificar todas las variables en el código y simplemente definirlas a priori.
Es mucho más fácil entrar en el archivo, modificar las variables, salvarlo y poner en la consola:
source("regresion-plot.R")
que tener que entrar el código paso a paso en la propia consola, con la posibilidad de errores que puede llevar. Si quiero gastar energías no es en revisar el código para ver donde me he podido equivocar, sino en interpretar las correlaciones y jugar con los datos.
Además para usuarios poco asiduos de R (como yo mismo si deseo reutilizar mi propio código), los comentarios y la división del programa en secuencias sencillas explicadas permite su lectura y evita problemas de sintaxis y de “picado” en la reprogramación.
La reutilización para dibujar regresiones de otro tipo, o para análisis más profundos es más fácil con este tipo de plantillas y las variables definidas inicialmente pueden servir para cualquier tipo de plot() o xyplot(), utilizando la libreria “lattice”.
Más artículos relacionados
Como entender intuitivamente que el resultado de empate de la asamblea de la CUP era el más probable
Construir una paleta de colores con R
Análisis de la conversación del “Sí” y “No” en twitter al anuncio de la consulta, el federalismo apenas participa en el debate de las opciones de voto
Creación con R de dendogramas semánticos y clústers de conversaciones en twitter
yo normalmente uso la funcion “glm” ya que tanto la regresión lineal, como la logaritmica u otras son casos especificos de los modelos lineales generalizados.
Amei:
He estado mirando la documentación de glm, y veo que no generaría demasiada distorsión respecto a la regresión con lm, si te parece bien, incluyo una línea comentada al lado de la regresión explicando que sea mejor utilizar glm.