Hace muy poco pedí la colaboración en un experimento a los lectores de mi blog. Engañé a los que participaron. La mentira tenía un interés científico ya que buscaba realmente, no la capacidad electoral predictiva intuitiva sino comprobar un efecto irracional que la economía del comportamiento llama “efecto ancla“. Este efecto ancla está comprobado para la fijación de precios o en las negociaciones, tanto en análisis como en experimentos de economía del comportamiento.

No conocía experimentos realizados sobre el efecto ancla alrededor de decisiones no puramente económicas (como la fijación de precios o la negociación) y me pareció interesante realizar un experimento para ver el efecto ancla en las espectativas de resultados electorales.

Daré una definición rápida del efecto ancla. Es un sesgo cognitivo irracional en el que una la presentación de una cifra previa que no tiene una relación causal o racional con el valor que queremos estimar nos termina de influir en la cifra que queremos estimar.

Un ejemplo de experimento que pone en relevancia el efecto ancla ha sido solicitar a los encuestados las dos últimas cifras del carnet de la seguridad social antes de valorar el precio de una botella de vino y ver que unas cifras altas en el carnet de la seguridad social otorgaba valores superiores al precio de una botella de vino. Algo totalmente irracional y aunque el conocimiento de los productos puede influir en reducir ese anclaje no termina de desaparecer.

¿Pero es posible que este efecto ancla se produzca en elementos con los que no nos vinculamos poniendo precios (y por tanto comparándolos con una hipotética escala de valor económico interna), sino haciendo estimaciones más o menos intuitivas?

Descripción del experimento sobre el efecto ancla en las espectativas de resultados electorales

A través de mi blog y los contactos en redes sociales lancé la petición de participar en una encuesta. El target que participó es el de lectores de mi blog y mis seguidores (y segunda corona) en las redes sociales, en general un colectivo muy interesado en la política y que se puede considerar bastante informado, con una porción no desdeñable en formación en ciencias sociales y con conocimiento de las últimas encuestas. Por tanto, un colectivo cuyo efecto de anclaje tendría que estar bastante apantallado. Al menos si seguimos las teorías racionales.

Los participantes fueron engañados en el propósito del estudio (perdón!!, lo tenía que hacer, pero desvelar el objetivo del estudio hubiera hecho inútil la encuesta). Se les hizo creer que participaban de un estudio de la capacidad predictiva electoral intuitiva y que se les solicitaba los dos primeros números del código postal para evitar sesgos por la provincia.

Se les hacía dos preguntas secuenciales, la primera se les pedía las primeras dos cifras (de las 5) del código postal, en la segunda que estimaran el resultado que tendría PODEMOS en las próximas elecciones generales. Ambas cifras son claramente no correlacionadas, pero al hacerlo secuencialmente, la primera podría provocar un sesgo por anclaje en la segunda y es lo que buscaba realmente el experimento.

Análisis del resultado.

El resultado fueron más de 251 respuestas, el grueso lo forman 131 de Barcelona (código 08) y 48 de Madrid (código 28) y 72 de otras provincias.

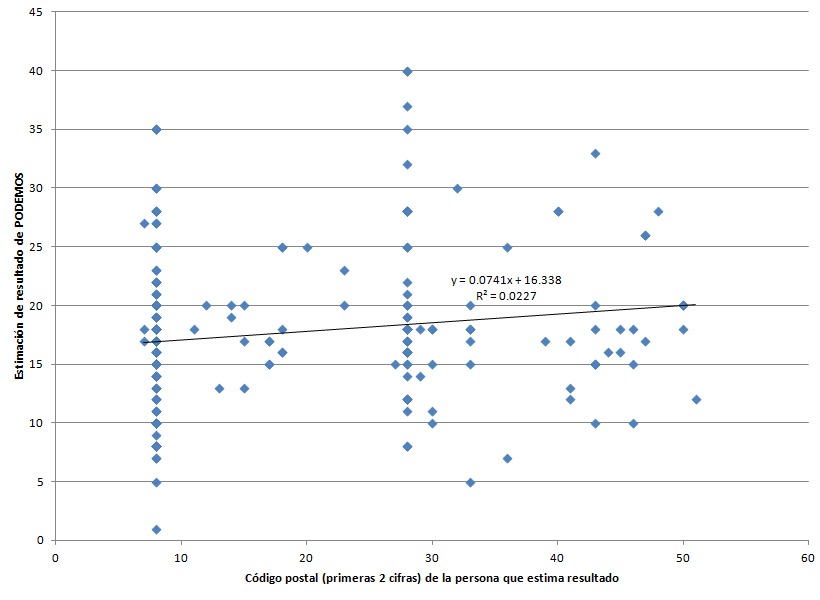
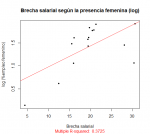
En una primera lectura de datos se buscó testear la hipótesis que el sesgo por anclaje basado en que a un código postal mayor se producirían predicciones más altas, y el resultado es el siguiente:

Hay una tendencia muy leve que relaciona códigos postales más bajos a predicciones más bajas y al revés, pero es muy poco relevante (un R^2 de 0,0227). El experimento parece que va al garete, existe efecto ancla pero sólo explicaría el 2% de variación.

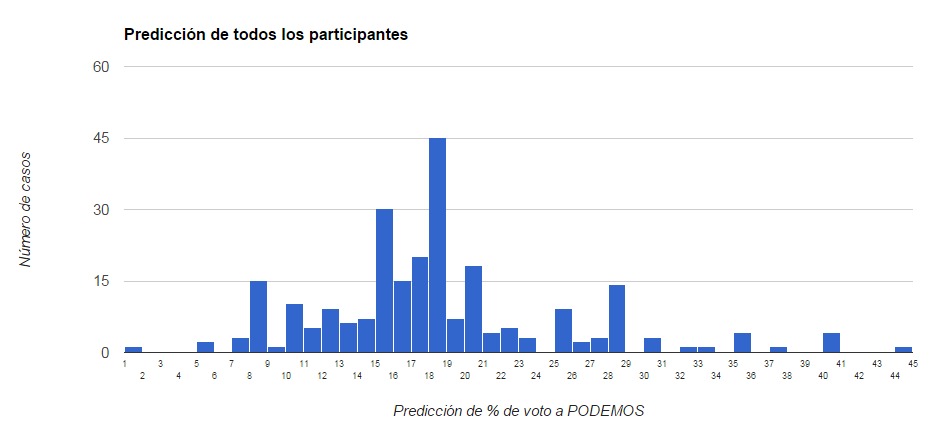
Pero un segundo análisis corresponde al histograma de respuestas y tenemos resultados sorprendentes.

Hay 3 picos anómalos que no corresponden a una curva gausiana o una curva de dispersión habitual alrededor de un valor mediano. Hay picos anómalos extremos en el 18, 15, 20, 28 y 8.

Después de analizar el conjunto de datos el 15 y el 20 se pueden explicar por la tendencia a hacer con más comodidad predicciones “redondeadas”, nos parece más razonable decir “15” o “20” en una predicción que 21 o 17, son números base y cómodos para nuestra base 10.

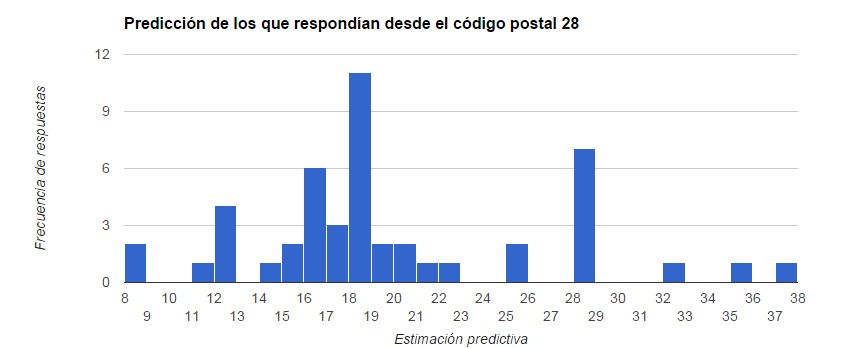
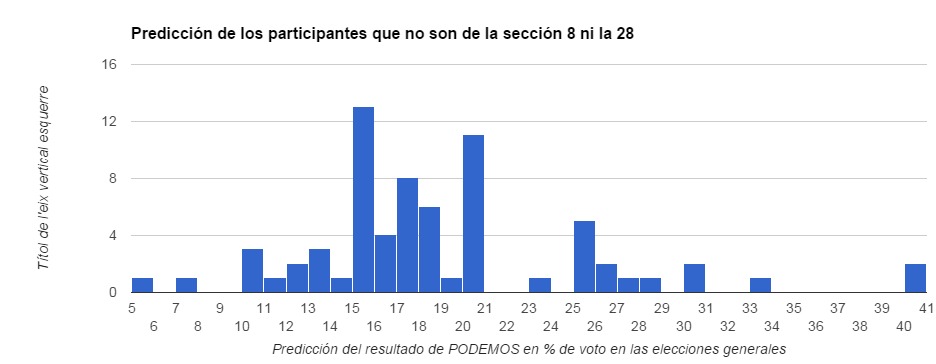
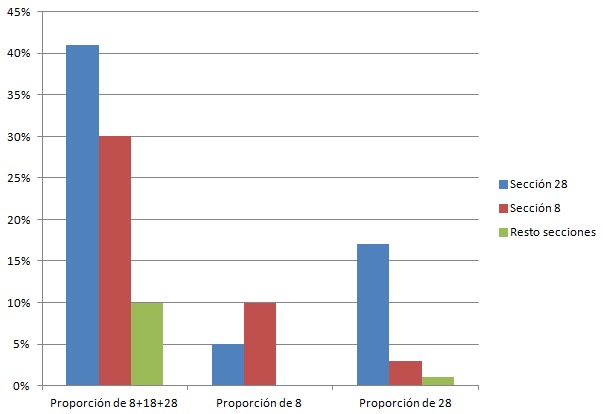
Pero el 8, 18 y 28 no tienen ninguna explicación, excepto… que la mayor parte de personas que hacen predicciones son de la sección 8 y de la 28. Si miramos las predicciones segregando los tres grupos (los de la sección 8, los de la sección 28 y los del resto de secciones vemos el siguiente resultado).

En el tercer caso que podemos definir como grupo de “control” al ser todos de secciones postales muy distintas, vemos que prevalece un valor medio alrededor del 17, con 4 picos anómalos, 10, 15, 20, 25 y dos algo más pequeño en el 30 y el 40. Lo esperable si no existe un sesgo de ancla (o este está tan disperso que queda apantallado) entre personas que piensan en números en base 10.

Pero el caso de la sección 8 y la 28, que son los que acumulan más participantes tiene un comportamiento anómalo. En la sección 28, los picos anómalos son el 18 y el 28, además del 15, en el caso de la sección 8 hay 3 picos anómalos, el 18, el 8 y uno menor en el 28, mientras aparecen los dos picos habituales del 15 y el 20.

Si miramos la proporción de predicciones acabadas en 8 (8, 18 y 28) entre la sección 8 y la 28 es bastante mayor que la del grupo de control del resto de secciones. También la prevalencia del ancla en la predicción dentro de las secciones 8 con el 8 y en el 28 con el valor 28, mayor que la del grupo de control.

El diferencial de respuestas “ocheras” afecta a entre el 20 y el 30% del total de respuestas para las que esperamos un efecto ancla. No es una influencia menor,  números poco racionales para el grupo de control como un resultado tan bajo como un 8% (de los que nadie responde en el grupo de control) o un resultado tan alto como un 28% (del que solo hay un único caso en el grupo de control) ha sido la respuesta automática de más del 10% de los que forman parte de esa sección. El valor del ancla, por muy irracional que fuera esa predicción es la respuesta automática que se ha producido en más del 10% de los casos.

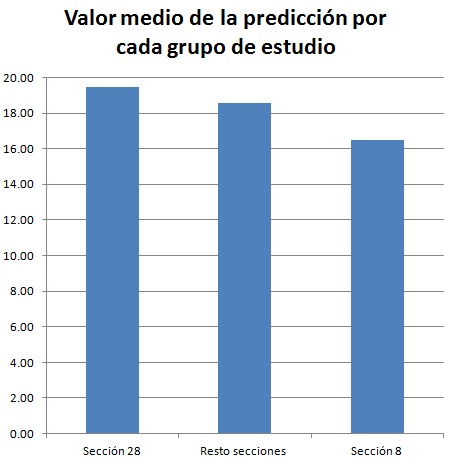
Aunque hemos comprobado que el ancla es poco explicativa para la dispersión de las predicciones que hacen los participantes del estudio, sí que una ancla mayor (28) fija una media de predicción más alta que el grupo de control, y que una ancla menor (8) fija una media de predicción más baja que el grupo de control. Se podría achacar a este diferencial medio al diferencial de percepción que se tiene de PODEMOS entre los madrileños y los barceloneses (en Madrid tienen más fuerza que en Barcelona), pero no quería dejar de remarcar que cuando se analiza en grandes grupos (por mala suerte no ha sido posible reunir muchas respuestas de otras secciones) sí que reaparece el efecto ancla clásico, aunque pueda tener en este caso una explicación fuera de la economía behavoriana y dentro de la politología.

Conclusión, no pienses en un 8

El efecto de ancla clásica es o muy débil o bien muy explicable por factores externos (diferencial de la fuerza de PODEMOS en Barcelona y Madrid), en este experimento es poco relavante.

Pero sí que se detecta otro efecto ancla alrededor de fijar los valores en la terminación común entre el ancla y el valor que se escoge, el efecto fijando resultados alrededor de unos valores cuya relación es irracional (lo que termina en 8), termina afectando al orden de entre el 30% y el 40% de las respuestas, un diferencial de entre el 20 y el 30% con respecto al grupo de control.

Además el valor del propio ancla, siendo casi totalmente irracional (respecto a las respuestas del grupo de control) es la respuesta de entre el 15 y el 10% de los que tienen ese ancla.

Mientras que un análisis de sesgos favorables al redondeo diría que el valor de anclaje debería fijarse en los valores terminados en 0 o en 5 (son valores a los que nuestras emociones nos predisponen), estamos viendo un efecto ancla superior incluso a la tendencia al redondeo (otro sesgo irracional bastante más estudiado que el efecto ancla).

Está claro que el efecto ancla se produce en las espectativas de resultados electorales, a pesar que no de la manera esperada. El pensar en un número aleatorio, en este caso algo acabado en un 8, genera respuestas sesgadas a favor del 8. Es un efecto palpable y poco discutible que termina afectando a un tercio de las respuestas.

Parafraseando a Lakoff, no pienses en un 8.